Il World Wide Locator o WWL, spesso chiamato semplicemente locator (traducibile con "localizzatore" e non con "locatore", che in italiano ha tutt'altro significato), è un semplice sistema per individuare la posizione geografica di una stazione radioamatoriale. Esso è conosciuto anche come Maidenhead Locator System, dal nome della località vicino a Londra dove il sistema fu concepito per la prima volta nel 1980, durante un incontro di responsabili VHF europei.

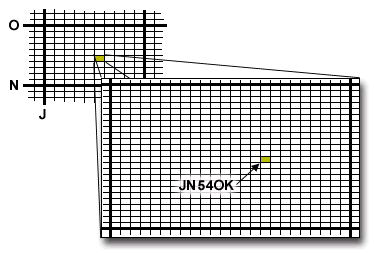
Ogni località della Terra può essere individuata da una stringa di 6 caratteri (due lettere + due numeri + due lettere), di cui le posizioni dispari specificano la longitudine e quelle pari la latitudine. Ad esempio il locator JN54OK individua Pontecchio Marconi, in provincia di Bologna (che ai radioamatori ricorda sicuramente qualcosa...).

Il funzionamento del World Wide Locator

Ogni coppia di caratteri identifica l'angolo inferiore sinistro di un "rettangolo" (in realtà, data la sfericità della Terra, quello di un "trapezio" curvilineo, che ai Poli diventa un triangolo).
La prima coppia di lettere suddivide la Terra in aree di larghezza pari a 20° di longitudine ed altezza pari a 10° di latitudine; la seconda coppia di numeri suddivide l'area così definita in aree più piccole di 2° di longitudine e 1° di latitudine e la terza coppia, infine, crea un'ulteriore suddivisione pari a 5 minuti di grado di latitudine e 2,5 minuti di grado di latitudine.
Usando la terminologia anglosassone, la prima coppia di lettere identifica il field, la coppia di numeri lo square e l'ultima coppia di lettere il subsquare. I valori di field e di square sono usati dai radioamatori anche per calcolare con maggior precisione le nazioni collegate.

Il sistema del WWL suddivide l'intera Terra con una griglia di 18.662.400 rettangolini.

Il calcolo delle coordinate

Per trasformare un valore WWL in latitudine e longitudine occorre innanzitutto sapere a cosa corrispondono le lettere e i numeri.

• La prima lettera indica la longitudine e varia da A a R. L'equivalenza è A=180° W, B=160° W, C=140° W, D=120° W, E=100 °W, F=80° W, G=60° W, H=40° W, I=20° W, J=0° o meridiano di Greenwich, K=20° E, L=40° E, M=60° E, N=80° E, O=100° E, P=120° E, Q=140° E, R=160° E.
• La seconda lettera indica la latitudine e varia da A a R. L'equivalenza è A=90° S, B=80° S, C=70° S, D=60° S, E=50 °S, F=40° S, G=30° S, H=20° S, I=10° S, J=0° o Equatore, K=10° N, L=20° N, M=30° N, N=40° N, O=50° N, P=60° N, Q=70° N, R=80° N.
• Il primo numero è il coefficiente (da 0 a 9) di incremento della longitudine, a passi di 2 gradi.
• Il secondo numero è il coefficiente (da 0 a 9) di incremento della latitudine, a passi di 1 grado.
• La penultima lettera indica il coefficiente (A=0, B=1, C=2, D=3, E=4, F=5, G=6, H=7, I=8, J=9, K=10, L=11, M=12, N=13, O=14, P=15, Q=16, R=17, S=18, T=19, U=20, V=21, W=22, X=23) di ulteriore incremento della longitudine, a passi di 5 minuti di grado.
• L'ultima lettera indica il coefficiente (da A = 0 a X = 23) di ulteriore incremento della latitudine, a passi di 2,5 minuti di grado.

Moltiplicando le varie suddivisioni (18 x 10 x 24) si vede che la Terra è suddivisa in 4.320 parti, sia lungo la latitudine sia lungo la longitudine.

La trasformazione del valore WWL nella latitudine e longitudine dell'angolo inferiore sinistro del rettangolino che contiene la stazione radio si ottiene sommando opportunamente i vari valori. Poi, dato che è più corretto dare le coordinate geografiche del centro del rettangolino, si aggiungono ancora 2,5 minuti di grado (pari a 2' 30") alla longitudine e 1,25 minuti di grado (pari a 1' 15") alla latitudine.

Pertanto le coordinate geografiche dell'angolo inferiore sinistro del rettangolino individuato dal nostro locator JN54OK sono:

• longitudine = 0° + 5 x 2° + 14 x 5' = 10° + 1°10' = 11° 10' E
• latitudine = 40° + 4 x 1° + 10 x 2,5' = 40° + 4° + 25' = 44° 25' N

Aggiungendo la correzione per individuare il suo centro queste coordinate geografiche si trasformano in 11° 12' 30" E, 44° 26' 15" N. Possiamo perciò dire che Pontecchio Marconi si trova dentro un'area di 5' di grado di longitudine e 2' 30" di latitudine il cui centro ha le coordinate geografiche appena calcolate.

Attraverso un procedimento inverso si può trasformare qualunque coppia di coordinate geografiche in un valore WWL.

La precisione del sistema WWL

Come detto, il WWL individua un'area e non un preciso punto geografico. Si pone perciò il problema di sapere qual è la sua precisione, ossia il margine d'errore di localizzazione. In altre parole, quanto può veramente distare, al massimo, la stazione radio dalla localizzazione virtuale individuata dal WWL?

Se la Terra fosse piatta, l'errore massimo sarebbe costante. In realtà, essendo la Terra "sferica" (per essere più precisi ha forma elissoidale, schiacciata ai Poli, ma per le nostre considerazioni possiamo considerarla come una sfera perfetta), la lunghezza dei paralleli varia con la latitudine. Perciò la lunghezza dell'arco di parallelo pari a 1° di longitudine sull'Equatore è maggiore di quella misurata su un parallelo alle nostre latitudini (45° N circa). La lunghezza dei meridiani è invece costante e la lunghezza pari a 1° di latitudine è sempre uguale. L'errore massimo si verifica quindi all'Equatore.
La lunghezza dell'Equatore si può considerare pari al doppio della lunghezza di un meridiano e in queste condizioni l'arco di 1' di grado di longitudine è uguale all'arco di 1' di grado di latitudine.
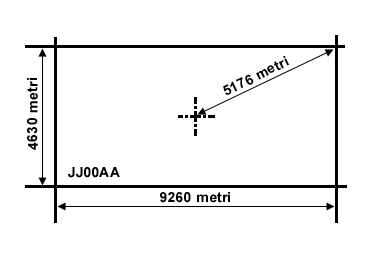
Dato che 1' di grado di latitudine è pari a 1 miglio marino, cioè 1852 metri, si ha che le dimensioni del rettangolino individuato dal WWL all'Equatore sono 9260 metri (= 1852 x 5) di larghezza e 4630 metri (= 1852 x 2,5) d'altezza.

Applicando la formula di Pitagora per i triangoli rettangoli si ottiene che il punto del rettangolino più lontano dal centro individuato dal WWL, ossia uno dei suoi angoli, dista dal centro circa 5176 metri. Si può perciò affermare che la precisione del WWL, nella peggiore delle ipotesi, è di circa 5 chilometri e che essa aumenta man mano che ci si avvicina ai Poli. Attenzione però: se due stazioni radio hanno lo stesso WWL la loro distanza reale può essere anche il doppio della precisione, nel caso in cui si trovino agli angoli opposti del rettangolino determinato dal WWL.

Utilizzando il calcolatore qui sotto potrete sapere qual è il massimo errore di localizzazione per un determinato valore di locator. Per semplicità è stato usato un modello sferico della Terra.

Per il calcolo automatico da coordinate a WWL e viceversa puoi usare questo software.