_________________________________________________

      Carta Di Smith  Generalità

 

La carta di Smith é uno strumento molto usato per risolvere tutti i problemi di adattamento delle linee a radiofrequenza.

La carta di SMITH è un diagramma circolare, costituito da due serie di circonferenze che si intersecano e che consentono di determinare l'impedenza, o più spesso, l'ammettenza, nelle sue due componenti reale ed immaginaria, della linea in ogni suo punto.

Si può, di conseguenza, scegliere il punto adatto lungo la linea, per inserire lo stub in grado di compensare la parte reattiva, indesiderata, del carico e permettere al generatore di vederne solo la parte resistiva e non dare, di conseguenza, onde riflesse indesiderate.

Si può adattare un carico anche se è soltanto resistivo, ma di valore diverso da quello della linea.

E' possibile adattare anche con l'uso di due diversi stub posti però a distanze dal carico opportunamente calcolate.

E' possibile, con la carta, calcolare anche la lunghezza che devono avere i singoli stub da inserire caso per caso.

Con la carta si calcola anche il coefficiente di riflessione ρ sul carico ed in ogni punto della linea, si rileva anche il ROS in ogni punto della linea ed anche del carico.

Con la carta si converte, a vista, un'impedenza nella corrispondente ammettenza. 
Si può tracciare il diagramma d’onda stazionaria determinando sia il ROS, sia la posizione dei massimi e dei minimi rispetto al carico.

La carta di Smith può essere usata, sia lavorando con le impedenze, che con leammettenze.

In ogni caso, tutte le grandezze sono normalizzate, cioè sono espresse come rapporto fra l'impedenza di carico e la resistenza caratteristica della linea, oppure come rapporto fra l'ammettenza di carico e l'ammettenza caratteristica della linea.

Non ci sono dunque, né valori in Ohm né in Siemens, ma solo numeri puri.

Anche le lunghezze, rappresentate da rotazioni angolari attorno al centro, sononormalizzate, non espresse in metri, ma misurate in parti di λ.

 

Descrizione Della Carta

 

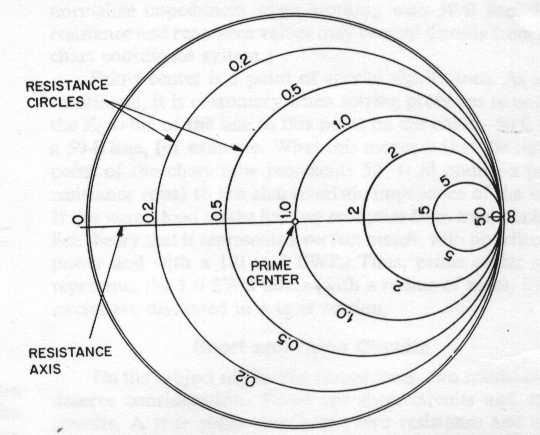
La carta è costituita da due serie di circonferenze, delle quali la prima, ha centri sull'asse orizzontale, la seconda ha centri sulla retta ad esso perpendicolare, passante per il suo estremo destro.

Ogni punto di ciascuna delle circonferenze della prima serie, rappresenta un punto della linea in cui l'impedenza ha parte reale costante, e questo valore è indicato sull'asse orizzontale.

Ogni punto di ciascuna delle circonferenze della seconda serie, rappresenta un punto della linea in cui l'impedenza ha parte immaginaria costante, il cui valore è indicato sulla circonferenza esterna, positiva al di sopra dell'asse orizzontale, e negativa al di sotto.

I centri di questi cerchi sono sulla retta perpendicolare al diametro orizzontale nel suo estremo destro.

L'origine del diagramma circolare è al centro, con il punto uno che rappresenta la parte finale di ogni adattamento, in quanto rappresenta quel punto della linea dove l'impedenza, complessivamente vista dal generatore, è uguale a quella caratteristica della linea, senza alcuna parte immaginaria, cioè si è finalmente adattato il carico.

Nella parte destra del diametro orizzontale sono rappresentati i numeri maggiori di uno e a sinistra i minori di uno, così all'estremità destra del segmento orizzontale è rappresentato il valore infinito e all'estremità sinistra il valore zero.

 

 

Esistono due versi di rotazione nella carta di Smith che corrispondono ai due versi possibili di percorrenza lungo la linea:

• uno orario, verso il generatore
• uno antiorario, verso il carico

Sul bordo esterno della carta sono rappresentati gli angoli in gradi e gli spostamenti lungo la linea, usando come misura, come già detto, la lunghezza d'onda della linea.
Lo spostamento lungo una linea in regime di onda stazionaria, da un minimo al successivo, e quindi di λ/2, comporta nella carta di Smith, la rotazione completa di 360° a partire da un punto sull’asse orizzontale a sinistra dell’origine.
Analogamente, lo spostamento da un massimo ad un altro massimo, comporta, nella carta di Smith, la rotazione completa di 360° a partire da un punto qualsiasi della parte destra dell’asse orizzontale.
Lo spostamento, invece, lungo una linea, da un minimo ad un massimo, comporta nella carta di Smith, la rotazione di 180° a partire da un punto sull’asse orizzontale a sinistra dell’origine, minimo, fino al punto simmetrico sull’asse orizzontale a destra, massimo.

 

Esempio Di Adattamento

Di Una Linea Con La Carta Di Smith

 

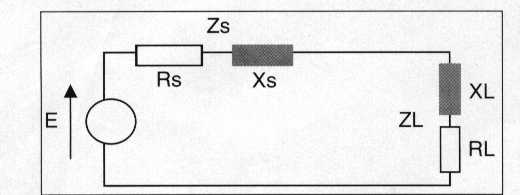
Sia data una linea con impedenza di carico ZL, da adattare con uno stub chiuso all'estremità, posto a distanza d1 dal carico e di lunghezza d2 secondo lo schema di figura:

Dati: R0 = 50 Ω; ZL= 60 + j 70 Ω; f = 27 MHz; v= 2x108m/sec

 

 

Per prima cosa bisogna normalizzare l'impedenza di carico ZL, dividendola per la resistenza caratteristica della linea R0:

 

Clicca sull'immagine per ingrandirla

A questo punto bisogna individuare il punto rappresentativo dell’impedenza di carico ZLall’interno della carta di SMITH, all’incrocio fra la circonferenza con parte reale +1,2 e la circonferenza con parte immaginaria +1,4.
Ricordiamo che i valori reali sono scritti sull’asse orizzontale, mentre quelli immaginari sono rappresentati lungo la circonferenza esterna, i positivi sopra, i negativi, sotto.
Il punto rappresentativo dell’impedenza di carico ZL è indicato nella figura di sopra.
Si traccia un cerchio (rosso) con centro nell’origine e passante per il punto ZL, il cui raggio rappresenterà il coefficiente di riflessione ρ in modulo e fase al variare del punto sulla linea supposta senza perdite.

Il modulo del coefficiente di riflessione ρ si legge proiettando il raggio del cerchio sulla scala orizzontale, che c’è sotto la carta, indicato con le due linee in blu, ottenendo il valore, indicato con il cerchietto blu, di 0,3. 
La fase, anch’essa indicata con un cerchietto blu, si legge sul bordo esterno della carta, sul prolungamento del raggio che passa per ZL e risulta quasi 50°.
La circonferenza, passante per il punto rappresentativo del carico ZL normalizzato, rappresenta tutti i punti della linea a partire dal carico, con i corrispondenti valori delle parti reali ed immaginarie dell’impedenza, che si possono ottenere spostandosi dal carico verso il generatore, ruotando in verso orario.

Vi sono due punti dove questa circonferenza interseca l’asse reale e corrispondono aimassimi, quelli a destra, ed ai minimi, a sinistra, dell’onda stazionaria, dove l’impedenza è puramente reale, che si alternano ogni λ/4.
In corrispondenza del massimo, a destra, si legge anche il valore del ROS che è di 3,4, indicato da un cerchietto nero.
Anche sulla scala in basso si può leggere lo stesso valore indicato con un altro cerchietto nero.
La distanza tra il carico ed il primo massimo dell’onda stazionaria, misurata, al solito in valori di λ, si trova ruotando in verso orario, dal punto rappresentativo dell’impedenza normalizzata ZL, fino al primo incontro con la parte destra dell’asse reale che, è indicata in figura con due cerchietti rossi:

 

Ribaltando rispetto al centro del diagramma circolare di Smith, il punto rappresentativo di ZLsi ottiene il punto rappresentativo dell’ammettenza di carico YL:

Per controllo, con la calcolatrice si ha:

 

Come si vede, esattamente uguale.  Questo è il punto di partenza per l’adattamento della linea.
Adesso agiamo con le ammettenze perché lo stub si dovrà inserire in parallelo e pertanto si dovranno sommare le ammettenze e non le impedenze.
Si ruota in verso orario, vale a dire verso il generatore lungo il cerchio rosso che è il cerchio a pari modulo di coefficiente di riflessione ρ, fino ad incontrare il cerchio a r=1, cioè il luogo dei punti in cui la parte reale dell’ammettenza è uguale ad uno.
Si osservi che ci sono due intersezioni fra questi due cerchi, per ogni rotazione completa attorno al centro della carta di SMITH.

Quindi, per ogni avanzamento di λ/2, a partire dal carico verso il generatore, ci sono due punti in cui l’ammettenza della linea mostra la stessa parte reale dell’ammettenza caratteristica.
Si sceglie il primo di questi punti incontrati girando in verso orario, indicato in figura con il punto A, e lì si inserirà lo stub in parallelo che dovrà annullare la parte immaginaria dell’ammettenza di linea.
Questa parte immaginaria di 1,3, è indicata con un cerchietto verde sul bordo esterno della carta, seguendo la circonferenza passante per A.
In questo modo, l’onda incidente dal generatore, arrivando in questo punto, e trovando un valore d’impedenza di linea uguale a quella caratteristica, non darà luogo ad onda riflessa e così la linea sarà adattata.

La distanza d1 tra il carico, rappresentato dal punto  YL ed il punto di inserzione dello stub, rappresentato dal punto A, si legge sul bordo esterno della carta come somma di due parti, in quanto le lunghezze, misurate in λ, hanno origine all’estremo sinistro del diametro orizzontale ed ivi anche finiscono.
Si deve dunque eseguire la somma di due parti:

•La prima va dal punto sulla circonferenza esterna, corrispondente ad  YL dove si legge0,432λ, fino all’estremo sinistro del diametro orizzontale, dove si legge 0,0λ.
•La seconda, dall’estremo orizzontale sinistro, dove si legge anche 0,0 λ, fino al prolungamento del punto A, dove si legge 0,171λ. 

Quindi risulta:

d1= (0,5 λ - 0,432 λ) + (0,171 λ - 0,0 λ) = 0,068 λ + 0,171 λ = 0,239 λ

La determinazione della lunghezza d2 dello stub, da inserire a distanza d1 dal carico, si esegue pure con l’uso della carta di SMITH come segue.
Si deve creare uno stub, chiuso ad un’estremità, che presenti all’ingresso una suscettanza di valore -1,3, uguale ed opposto a quella letta sulla carta.
Lo stub in corto circuito, è anch’esso una linea a radiofrequenza, ma che ha come carico un corto circuito, cioè un’impedenza di valore zero, e quindi un’ammettenza di valore infinito.

Si parte allora dal punto più a destra dell’asse orizzontale delle parti reali della carta, che rappresenta appunto il valore infinito, e si segue il cerchio esterno della carta, ruotando in verso orario, quindi verso il generatore, fino a incontrare il punto, indicato sul bordo esterno con un cerchietto verde, corrispondente al valore di –1,3.
Si ricorda che nel semipiano inferiore i valori immaginari sono negativi ed in quello superiore sono positivi.
La lunghezza d2 dello stub, espressa in unità λ, è rappresentata dall’angolo compreso fra il punto rappresentativo del corto circuito ed il punto ad ammettenza –1,3.
Questa lunghezza si ottiene dalla differenza fra i valori letti nelle due posizioni corrispondenti al corto circuito, cioè, al carico, ed al punto di ingresso dello stub, indicate dai due cerchietti marrone e corrisponde al valore:

 

I valori di lunghezze fin qui ottenuti sono espressi in quote parti di λ, per trasportarli in metri bisogna calcolare λ:

 

Conosciuto il valore di λ, si può risalire ai valori in cm di d1 e di d2:

 

 

__________________________________________________

 

 

 

Smith Chart

                                                                                                                                                                Named after its inventor, Phillip H. Smith ( Bell Laboratories), the Smith Chart was originally described in Electronics for January 1939.

• Smith Chart it is a graphic tool for solving transmission lines problems.

• One of the simpler applications is to determine the feed point impedance of an antenna, based on an impedance measurement at the input of an random length of transmission line.

• The Smith Chart may be used for other proposes too, such as the design of impedance-matching networks. These matching networks can take on any of several forms, such as L and Pi networks, a stub matching system, a series-section match, and more.

• Impedance matching is often necessary in the design of RF circuitry to provide the maximum possible transfer of the power between a source and its load. The source impedance must equal the complex conjugate of load impedance, or:

 Rs + jXs = RL - jXL

• The input impedance, or the impedance seen when “looking into” a length of line, is dependent upon the SWR, the length of the line, and the Zo of the line. The SWR, in turn, is dependent upon the load, which terminates the line. There are complex mathematical relationships which may be used to calculator the various values of impedances, voltages, currents, and SWR values that exist in the operation of particular transmission line.

• The Smith Chart is developed by examining the load where the impedance must be matched, and is really nothing more than a specialized graph. Consider it as having curved, rather than rectangular, coordinate lines. The coordinate system consists simply of two families of circles, the resistance family, and the reactance family. The resistance circles are centred on the resistance axis (the only straight right of the chart). Each circle is assigned a value of resistance, which is indicated at the point where the circle crosses the resistance axis. All points along any one circle have the same resistance value. As with the resistance circles, the values assigned to prime center. Values to the top of the resistance axis are positive (inductive), and those to the bottom of the resistance axis are negative (capacitive).
  When the resistance family and the reactance family of circles are combined, the coordinate system of the Smith Chart results. Complex impedances (R + jX) can be plotted on this coordinate system.

 

 

     For better understanding let give an example. Suppose we have an impedance consisting of 50 ohms resistance and 100 ohms inductive reactance (Z = 50 +j100). If we assign a value of 100 ohm to prime center, we normalize the above impedance by dividing each component of the impedance by 100 (Normalization must be used, in order to facilitate the plotting of larger impedances. Each impedance to be plotted is divided by a convenient number that will place the new normalized impedance near the center of the chart where increased accuracy in plotting is obtained). The normalized impedance is then 50/100 + j(100/100) =
0.5 + j1.0. This impedance is plotted on the Smith Chart at the intersection of 0.5 resistance circle and the +1.0 reactance circle.
    Instead of assigning 100 ohms to prime center, we assign a value of 50 ohms. With this assignment, the 50 + j100 ohm is plotted at the intersection of the
50/50 = 1.0 resistance circle, and the 100/50 = 2.0 positive the same impedance value, 50 + j100 ohms. This example shows that the same impedance may be plotted at different points on the chart, depending upon the value assigned to prime center. But two plotted points cannot represent the same impedance in the same time.
Prime center is a point of special significance. It is customary when solving problems to assign the Zo value of the line to this point on the chart, 50 ohms for a 50 ohms line, for example. The center point of the chart now represents 50 + j0 ohms, a pure resistance equal to the characteristic impedance of the line, that it represents a perfect match, with no reflected power and with a 1.0 to 1 SWR.
    When plotting impedances two cases can be. These are short circuits and open circuits. A true short circuit has zero resistance and zero reactance, or 0 + j0. This impedance is plotted at the left of the chart, at the intersection of the resistance and reactance axes. An open circuit has infinite resistance, and therefore is plotted at the right of the chart, at the intersection of resistance and reactance axes.

 

                   

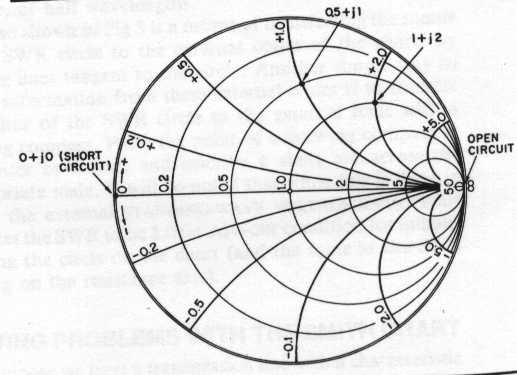
    In other words the zero ohms circles (r = 0) is the largest one and the infinite resistor circle is reduced to one point at (1,0). There should be no negative resistance. If one (or more) should occur, we will be faced with possibility of oscillatory conditions.
     It can be seen that all of the circles of one family will intersect all of the circles of the other family. Knowing the impedance, in form of: r + jx, the corresponding reflection coefficient can be determined. It is only necessary to find the intersection point of the two circles, corresponding to the values r and x.
    The reverse operation is also possible. Knowing the reflection coefficient, find the two circles intersecting at that point and read the corresponding values r and x on the circles. The procedure for this is as follows:
 
    - Determine the impedance as a spot on the Smith Chart
    - Find the reflection coefficient Γ (Gamma) for the impedance.
The reflection coefficient is defined as the ratio between the reflected voltage wave and the incident voltage wave:

Gamma = Vref / Vinc
    - Having the characteristic impedance and Γ (Gamma), find the impedance
Any point on the Smith Chart represents a series combination of resistance and reactance of  Z = R + jX. 

Thus , to locate the impedance Z = 1 +j1, you would find R = 1 constant resistance circle and follow until it crossed the X = 1 constant reactance circle. The junction of these two circles would then represent the needed impedance value)
    - Convert the impedance to admittance.
The equivalent admittance of a plotted impedance value lies diametrically opposite the impedance point on the chart. In other words, an impedance plot and its corresponding admittance plot will lie on a straight line then passes through prime center, and each point will be the same distance from prime center (on the same SWR circle)
    - Find the equivelent impedance.
    - Find the components values for the wanted reflection coefficient
 
    The third family of circles, which are not printed on the main chart, but are added during the process of solving problems, are SWR circles. Each circle represents a value of SWR, with every point on a given circle representing the same SWR. The SWR for a given circle may be determined directly from the chart coordinate system, by reading the resistance axis to the right prime center.

 

     

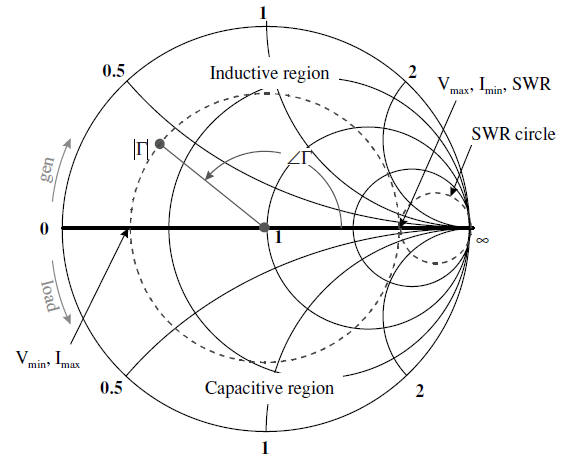
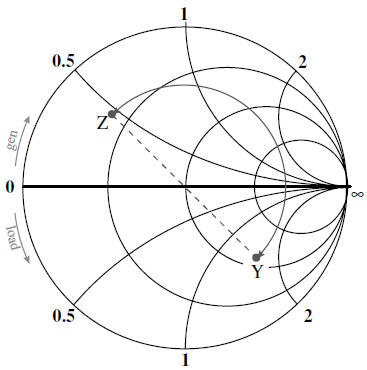
The Smith Chart has the following futures:

• It represents all passive impedances on a grid of constant r and x circles.

• It contains the corresponding reflection coefficients in polar co-ordinates; the angle being read on the peripheral scale and the magnitude being calculated using:

  

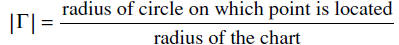
• The upper half of the diagram represents positive reactance values (inductive elements).

• Impedance or Admittance values read from the chart are normalized values.

• Moving away from the load (i.e. toward the generator) corresponds to moving in a clockwise direction.

•  A complete revolution around the chart is made moving a distance L = λ/2 along the transmission line.

• The same chart can be used for reading admittance.

• The center of the chart corresponds to the impedance-matched condition since Γ = 0.

• A circle centered at the origin is a constant Γ circle.

• Moving along the lossless transmission line is equivalent to moving along Γ circle.

• For impedance Z reading, the point (Γ_r = 1 and Γ_i = 0) corresponds to an open circuit.

• For admittance Y reading, the same point corresponds to a short circuit.

• The impedance distance λ/4 from Z_L is equal to Y_L.

• The SWR can be found by reading R at the intersection of the constant Γ circle with real axis.

• The Smith Chart can be used to find: Γ_L from Z_L and vice-versa, Z_in from Z_L and vice-versa, Z from Y and vice-versa, the SWR, and the impedance matching.

• The horizontal radius to the left of the centre corresponds to voltage minimum and current maximum (V_min, I_max).

•  

   

• The lower half of the diagram represents negative reactance values (capacitive elements).

• The horizontal radius to the right of the centre corresponds to the standing wave ratio (SWR), the voltage maximum and the current minimum (Vmax, Imin).

      

References:
    1. RF Circuit Design - C. Bowick

    2. RF and Microwave Wireless Systems - K. Chang

    3. Microwave Communications Engineering - Glover, Pennock, Shepherd

    4. RF Design Magazine, 1988-2000
    5. Microwave Journal, 1998-2000
    6. Applied Microwave Magazine, 1995-2000
    7. ARRL Handbook, 1990-2000

 

Iulian Rosu, YO3DAC / VA3IUL