|
|
Formule Geometriche
Rettangolo di base b e altezza a

Parallelogramma di base b e altezza h
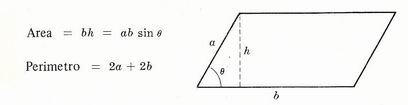
Triangolo di base b e altezza h
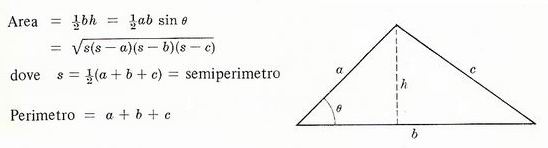
Trapezio di basi a e b e altezza h
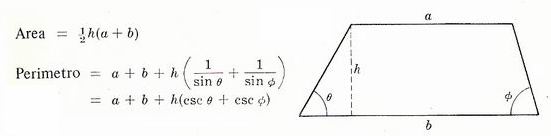
Poligono regolare di n lati ognuno di lunghezza b
Cerchio di raggio r
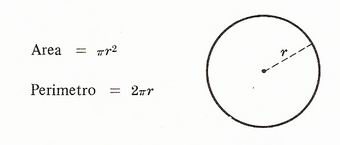
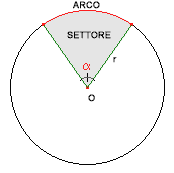
Settore circolare di raggio r

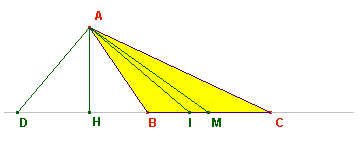
Raggio del cerchio inscritto di un triangolo di lati a, b, c

Raggio del cerchio circoscritto a un triangolo di lati a, b, c

Poligono regolare di n lati inscritto in un cerchio di raggio r
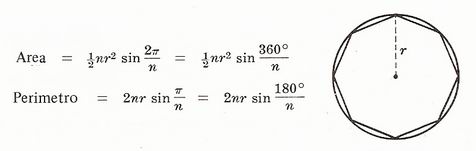
Poligono regolare di n lati circoscritto in un cerchio di raggio r
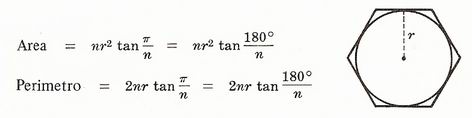
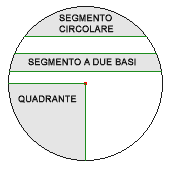
Segmento circolare di raggio r
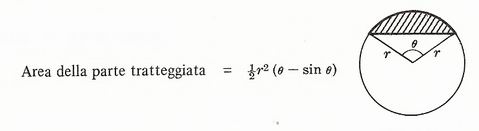
Ellisse di semiasse maggiore a e semiasse minore b

Segmento di parabola
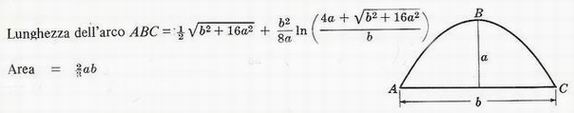
Parallelepipedo rettangolo di lunghezza a, altezza b e profondità c
Parallelepipedo con area della sezione A e altezza h

Sfera di raggio r
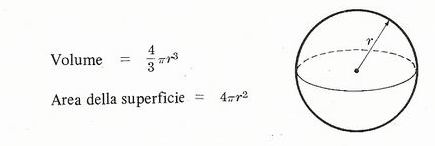
Cilindro circolare retto di raggio r e altezza h

Cilindro circolare retto di raggio r e generatrice l
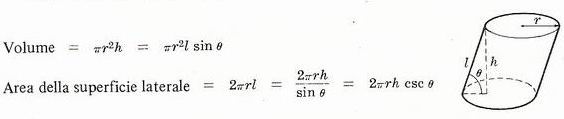
Cilindro con area della sezione A e generatrice l
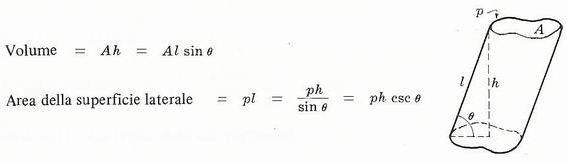
Cono circolare retto di raggio r e altezza h
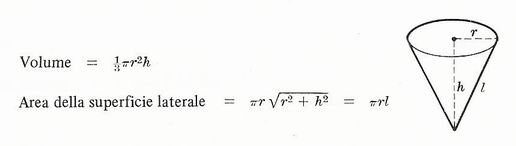
Piramide con area di base A e altezza h
Calotta sferica di raggio r e altezza h

Tronco di cono circolare retto di raggi a, b e altezza h
Triangolo sferico di angoli A, B, C su una sfera di raggio r
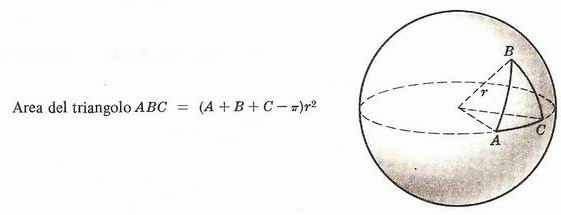
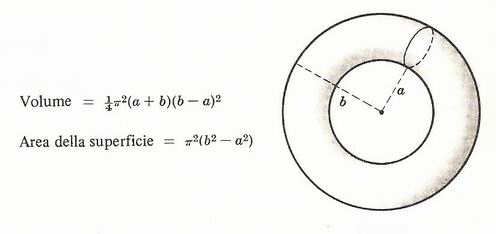
Toro di raggio interno a e raggio esterno b
Ellissoide di semiraggi a, b, c

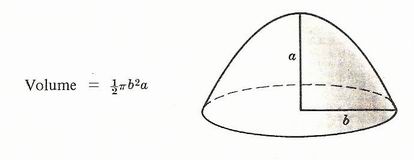
Paraboloide di rivoluzione
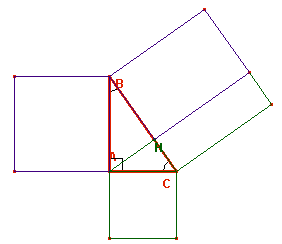
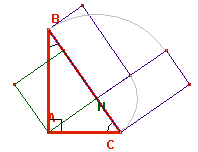
Triangoli rettangoli
|
|
LEGENDA
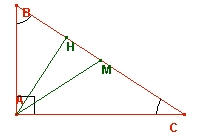
AB = c (cateto), AC = b (cateto), BC =
a (ipotenusa)
BÂC =
a = 90°, ABC = b, ACB = g
AH = h, altezza
AM = m, mediana
A = area
|
|
» Teorema di Pitagora:
In un triangolo rettangolo il quadrato costruito sull’ipotenusa
è equivalente alla somma dei quadrati costruiti sui due cateti.
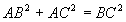
|
|
|
» 1° Teorema di Euclide:
In un triangolo rettangolo il quadrato costruito su un cateto è
equivalente al rettangolo che ha per dimensioni la sua proiezione sull’ipotenusa e l’ipotenusa stessa.
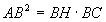 ; ; 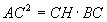
|
|
» 2° Teorema di Euclide:
In un triangolo rettangolo l’altezza è media proporzionale tra
le proiezioni dei due cateti sull’ipotenusa.
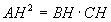
|
|
» Proprietà della mediana:
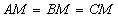
|
|
» Calcolo dell’area:
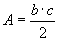 , , 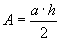
|
|
» Misura dell’altezza noti i lati:
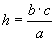
|
|
» Relazione fra i lati e il raggio della
circonferenza inscritta:
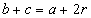
|
|
» 1° teorema sui triangoli
rettangoli:
In un triangolo rettangolo la misura di un cateto è uguale al
prodotto dell’ipotenusa per il seno dell’angolo opposto o per il coseno dell’angolo adiacente
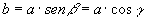 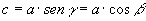
|
|
, » 2° teorema sui triangoli
rettangoli:
In un triangolo rettangolo la misura di un cateto è uguale al
prodotto dell’altro cateto per la tangente dell’angolo opposto o per la cotangente dell’angolo adiacente
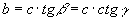 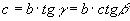
|
|
Triangoli qualsiasi
|
|
LEGENDA
AB = c, AC = b,
BC = a
BÂC = a, ABC = b, ACB = g
AH = h, altezza
AM = m, mediana
AI = l, bisettrice
AD = bisettrice angolo esterno
p = ½(a + b + c),
semiperimetro
A = area
|
|
» Proprietà:
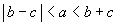 , , 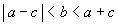 , , 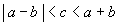

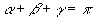
|
|
» Calcolo dell’area:
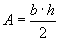
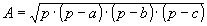 formula di
Erone formula di
Erone
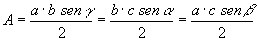
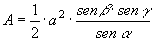
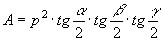
|
|
» Lunghezza delle mediane:
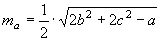 , , 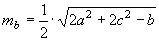 , , 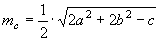
|
|
» Teorema della mediana:
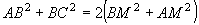
|
|
» Bisettrici:
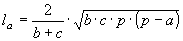 , , 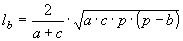 , , 
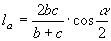 , ,
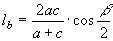 , ,
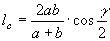
|
|
» Teorema della bisettrice dell’angolo
interno:
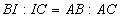
|
|
» Teorema della bisettrice dell’angolo
esterno:
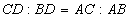 (se i segmenti
esistono) (se i segmenti
esistono)
|
|
» Raggio della circonferenza
circoscritta:
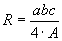 ,
,
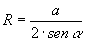 , , 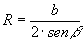 , , 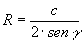
|
|
» Raggio della circonferenza inscritta:
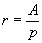 , , 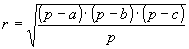 , ,
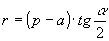 , , 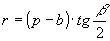 , , 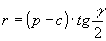
|
|
» Raggio delle circonferenze
exinscritte:
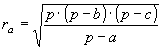 , , 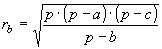 , , 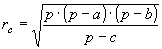
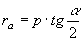 , , 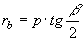 , , 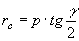
|
|
» Altezze:
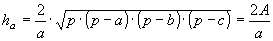 , ,
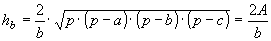 , ,
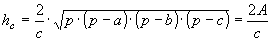
|
|
» Teorema dei seni (o di Eulero)
In un triangolo è costante il rapporto tra la misura di
un lato e il seno dell’angolo opposto:
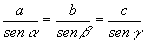
» Teorema della corda
In un triangolo il rapporto tra la misura di un lato e il seno
dell’angolo opposto è uguale al diametro della circonferenza circoscritta:
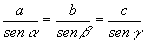 =
2r =
2r
|
|
» Teorema delle proiezioni:
In un triangolo qualunque, la misura di un lato è uguale alla
somma dei prodotti delle misure di ciascuno degli altri due per il coseno degli angoli che essi formano con il primo.
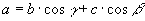 , , 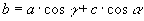 , , 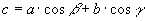
|
|
» Teorema del coseno (o di Carnot)
In un triangolo il quadrato di un lato è uguale alla somma dei
quadrati degli altri due diminuita del prodotto di questi due lati per il coseno dell’angolo fra essi compreso:
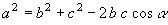 , ,
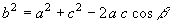 , ,
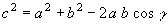 . .
|
|
» Formule di Briggs:
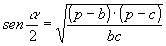 , , 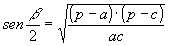 , , 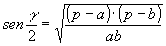
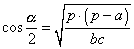 , , 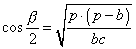 , , 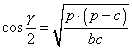
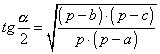 , , 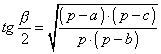 , , 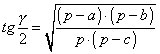
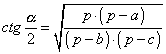 , , 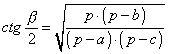 , , 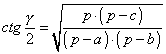
|
|
» Teorema delle tangenti (o di
Nepero)
In un triangolo qualunque la somma di due lati sta alla loro
differenza come la tangente della semisomma degli angoli opposti ai suddetti lati sta alla tangente della loro semidifferenza:
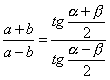
che si può anche scrivere: 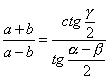
|
Cerchio e Circonferenza
|
Lunghezza della circonferenza: 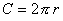
Area del cerchio: 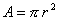
Lunghezza dell’arco: 
Area del settore circolare: 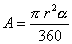
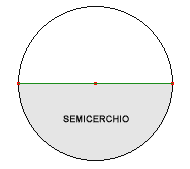
Area del semicerchio: 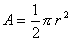
Area del quadrante: 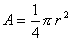
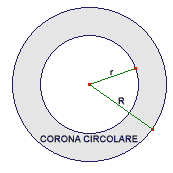
Area della corona circolare: 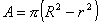
Area del segmento circolare: si trova come
differenza fra l’area di un settore e l’area di un triangolo.
|
LEGENDA
Raggio = r
|
|
» Teorema della corda:
(vedi anche il terorema dei seni)
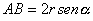
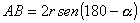
dove 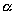 è uno qualsiasi
degli angoli alla circonferenza inscritti nell’arco maggiore AB . è uno qualsiasi
degli angoli alla circonferenza inscritti nell’arco maggiore AB .
|
|
|
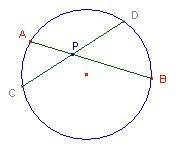
» Teorema delle
corde:
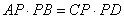 , ossia , ossia
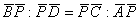
|
|
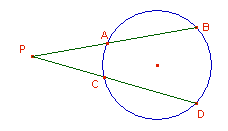
» Teorema delle
secanti:
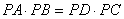 , ossia , ossia
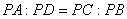
|
|
» Teorema della tangente e della
secante:
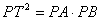 , ossia , ossia
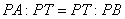
|
Quadrilateri
|
|
LEGENDA
AB
= c, BC = b, CD = a, DA = d,
DMC = a,
p = semiperimetro
|
» Calcolo
dell’area:
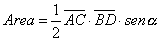
» Condizione di
inscrittibilità:
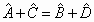
» Condizione di
circoscrittibilità:
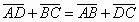
|
|
» Formule relative al
quadrilatero inscrittibile:
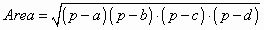 (Formula di Brahmagupta) (Formula di Brahmagupta)
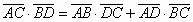 (Teorema di Tolomeo) (Teorema di Tolomeo)
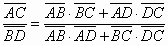 (Teorema di Legendre) (Teorema di Legendre)
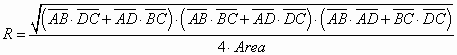 Raggio della circonferenza circoscritta Raggio della circonferenza circoscritta
|
|
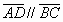
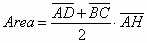
» Trapezio
isoscele
» Trapezio
isoscele
» Proprietà del trapezio
isoscele:
- Gli angoli alle basi
sono uguali
- Il lato obliquo di un trapezio isoscele circoscritto ad un semicerchio è uguale alla metà della base
maggiore
- Il lato obliquo di un trapezio isoscele circoscritto ad una circonferenza è uguale alla semisomma delle
basi del trapezio stesso.
» Trapezio rettangolo: è un
particolare trapezio in cui un lato è perpendicolare alle basi
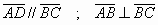
|
|
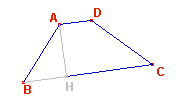
Quadrilatero
particolare. Trapezio (una coppia di lati sta su rette tra loro
parallele).
|
|
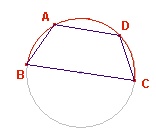
Quadrilatero
particolare. Trapezio isoscele (i lati obliqui sono tra loro
congruenti).
|
|
|
» Parallelogramma: è un
quadrilatero con i lati opposti paralleli
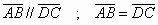
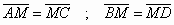
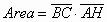
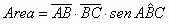
» Proprietà del
parallelogramma:
- Gli angoli opposti sono uguali e gli adiacenti sono supplementari
- Ogni diagonale scompone il parallelogramma in due triangoli uguali
- Le diagonali si tagliano scambievolmente per metà
|
|
|
Quadrilatero
particolare. Trapezio particolare. Parallelogramma (i lati opposti sono
congruenti e stanno su rette tra loro parallele).
|
|
|
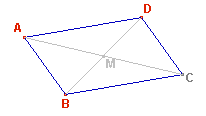
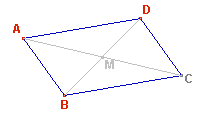
» Rombo: è un parallelogramma
particolare in cui i quattro lati sono uguali
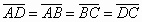
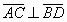
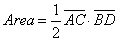
» Proprietà del rombo:
- Gli angoli opposti
sono uguali e gli adiacenti sono supplementari
- Le diagonali si tagliano scambievolmente per metà e sono fra loro perpendicolari
- Le diagonali sono bisettrici degli angoli, i cui vertici sono gli estremi delle
diagonali
|
|
|
Quadrilatero
particolare. Parallelogramma particolare. Rombo (i lati sono
tra loro congruenti e le diagonali stanno su rette tra loro perpendicolari).
|
|
|
» Rettangolo: è un parallelogramma
particolare in cui i lati adiacenti sono tra loro perpendicolari
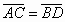
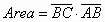
» Quadrato: è un rombo
particolare in cui i lati adiacenti sono tra loro perpendicolari
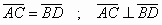
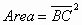
|
|
|
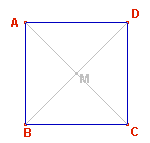
Quadrilatero
particolare. Rombo particolare. Quadrato (è un rombo in cui
i lati adiacenti sono tra loro perpendicolari).
|
|
'); //--> 
|
|
|
|
![]() =
= ![]()
 = 0,318 x C
= 0,318 x C
 =
= ![]()
 = 0,159 x C
= 0,159 x C
 = 0,758 x d2
= 0,758 x d2
 = 0,250 C x d
= 0,250 C x d
 = 0,707 x d
= 0,707 x d
 = 3,141 592 653 589 793...
= 3,141 592 653 589 793...
 D= diametro maggiore d=diametro minore s=superficie (parte nera)
D= diametro maggiore d=diametro minore s=superficie (parte nera)
![]() (D2-d2)
(D2-d2)
















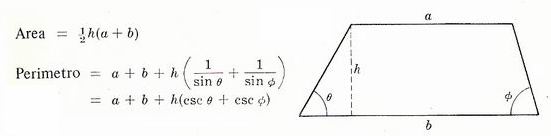
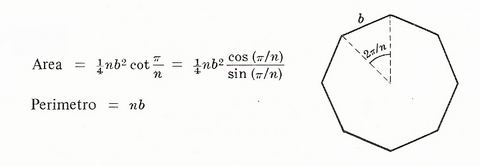




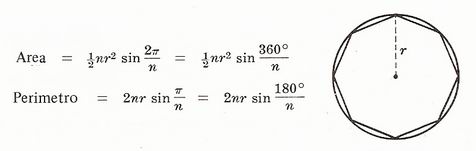
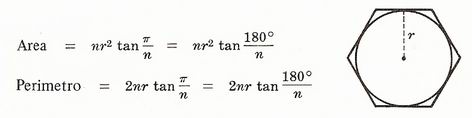
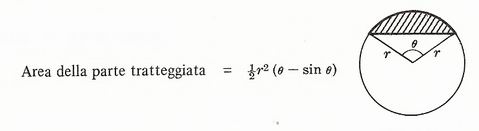

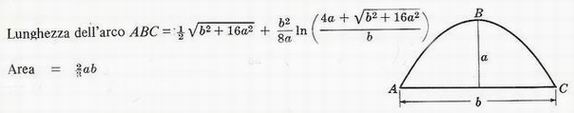
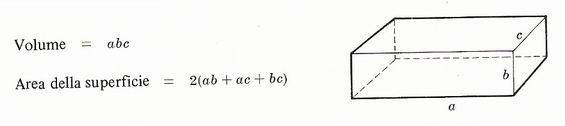

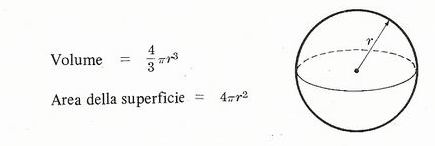

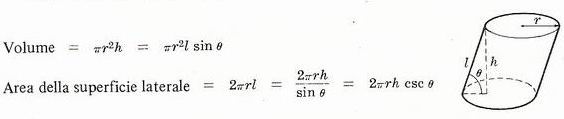
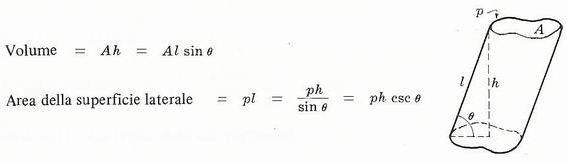
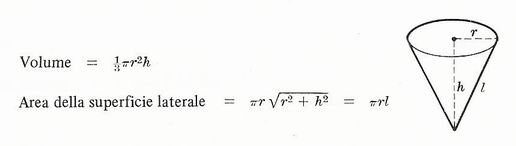


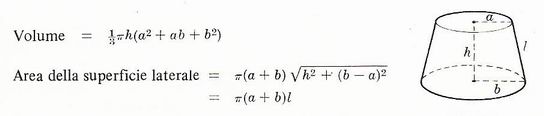
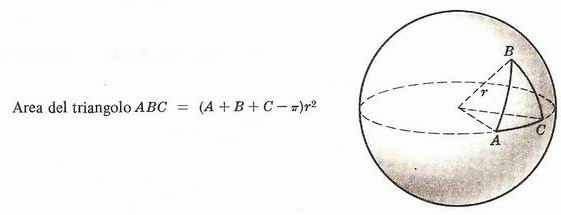



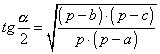 ,
, 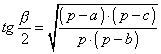 ,
, 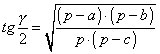
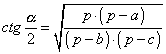 ,
, 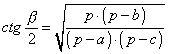 ,
, 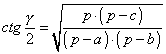
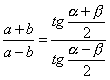
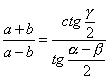
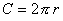
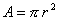

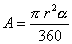
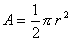
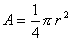
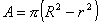
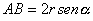
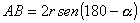
 è uno qualsiasi
degli angoli alla circonferenza inscritti nell’arco maggiore AB .
è uno qualsiasi
degli angoli alla circonferenza inscritti nell’arco maggiore AB .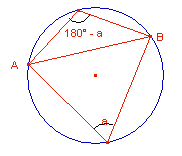
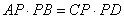 , ossia
, ossia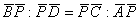
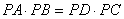 , ossia
, ossia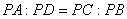
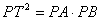 , ossia
, ossia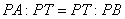
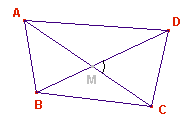
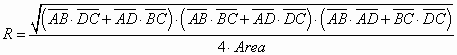 Raggio della circonferenza circoscritta
Raggio della circonferenza circoscritta



